Skip to contents

The Generalized logistic distribution

distrib.Rd

Density, distribution function, quantile function and random generation a generalized logistic distribution.

Usage

pgenlog(q, a = sqrt(2/pi), b = 0.5, p = 2, mu = 0, lower.tail = TRUE)

dgenlog(x, a = sqrt(2/pi), b = 0.5, p = 2, mu = 0)

qgenlog(k, a = sqrt(2/pi), b = 0.5, p = 2, mu = 0, lower.tail = TRUE)

rgenlog(n, a = sqrt(2/pi), b = 0.5, p = 2, mu = 0)

Arguments

a, b, p

parameters \(\ge 0\), with restrictions.*

mu

mu parameter

lower.tail

logical; if TRUE (default), probabilities are \(P[X \le x]\) otherwise, \(P[X > x]\).

x, q

vector of quantiles.

k

vector of probabilities.

n

number of observations. If length(n) > 1, the length is taken to be the number required

Value

dgenlog gives the density, pgenlog gives the distribution function, qgenlog gives the quantile function, and rgenlog generates random deviates.

The length of the result is determined by n for rgenlog, and is the maximum of the lengths of the numerical arguments for the other functions.

Details

The used distribution for this package is given by: $$f(x) = ((a + b*(1+p)*(|x-mu|^p))*exp(-(x-mu)*(a+b*(|x-mu|^p)))) / ((exp(-(x-mu)*(a + b* (|x-mu|^p)))+1)^2)$$

The default values for a, b, p and mu produces a function with mean 0 and variance close to 1.

*Restrictions:

If p equals to 0, b or a must be 0 otherwise there is identifiability problem.

The distribution is not defined for a and b equal to 0 simultaneously.

References

Rathie, P. N. and Swamee, P. K (2006) On a new invertible generalized logistic distribution approximation to normal distribution, Technical Research Report in Statistics, 07/2006, Dept. of Statistics, Univ. of Brasilia, Brasilia, Brazil.

Examples

pgenlog(0.5) 
#> [1] 0.6133563
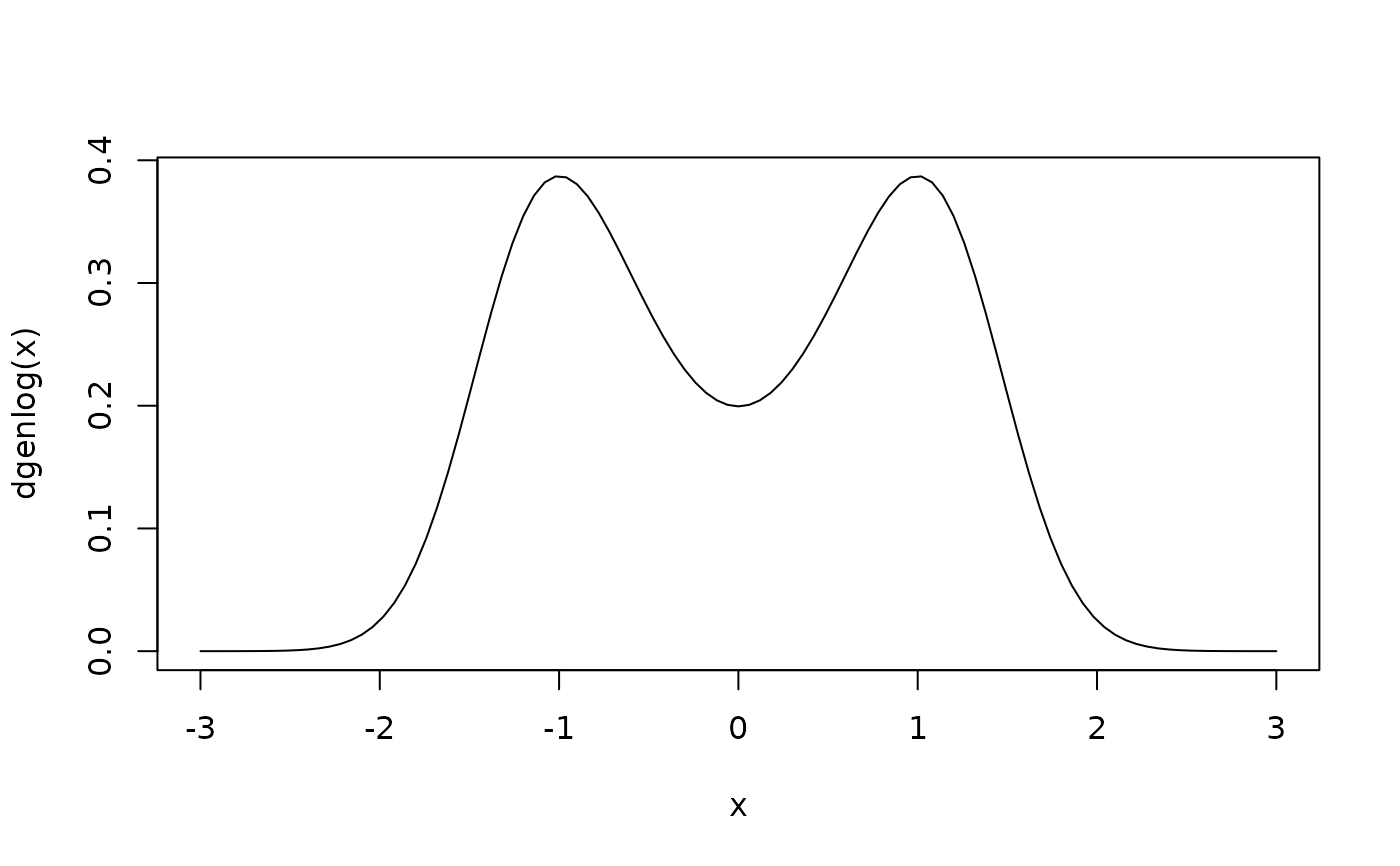
curve(dgenlog(x), xlim = c(-3,3)) 


rgenlog(100) 
#>   [1] -1.384665536  1.127636944  0.453645443 -1.150411842 -1.892490321
#>   [6] -0.165871481 -0.011141693 -0.801253961  0.862660824  0.966515316
#>  [11]  1.239865214 -1.102993992 -1.603206004 -0.714199084 -0.441937701
#>  [16] -1.048771598 -0.437314739 -1.451812742 -0.492574066  1.675029441
#>  [21] -0.800909063  0.710568524  0.869156101 -1.048026855  1.720607255
#>  [26]  0.885600691 -1.507183733  0.149550757  0.760965280  0.740202652
#>  [31] -1.623443098 -0.971471722 -0.770418068  0.579788897 -0.104501393
#>  [36] -0.321354435  0.790735545  1.507294915 -1.088777022 -0.993856779
#>  [41]  0.715810182 -0.005787101  0.596950035  0.655998551 -1.331362935
#>  [46]  0.948582653  0.959145549  1.854691677  1.635889858 -0.490827382
#>  [51] -0.190632331 -0.729222936 -1.103693469  0.156112736 -0.031880572
#>  [56]  0.984062837 -1.026727218  0.809962172 -1.445274335 -0.610292379
#>  [61]  1.103364026 -0.844703743  0.330793068 -0.668275280  0.436551020
#>  [66] -1.059561616  1.503354763  0.207851761  0.217734486 -0.831795571
#>  [71] -0.257511610 -0.552960625 -1.646382761 -0.167816779 -0.487743758
#>  [76] -1.714627000 -0.534176272  0.286993560  1.189732366 -0.506569894
#>  [81]  0.138437467  0.453181111 -0.877944176 -0.800472888 -0.099326472
#>  [86]  1.387442687 -0.448048524 -1.003482926  0.690919054 -1.473765624
#>  [91]  2.033888226 -1.172751220  0.092574240  1.159466417  0.823282964
#>  [96] -0.930609252  0.229011995  1.128890543 -1.647175059 -0.151496981

qgenlog(0.95)
#> [1] 1.5143