Skip to contents

The Generalized logistic distribution with skewness

distrib_sk.Rd

Density, distribution function, quantile function and random generation a generalized logistic distribution with skewness.

Usage

pgenlog_sk(
  q,
  a = sqrt(2/pi),
  b = 0.5,
  p = 2,
  mu = 0,
  skew = 0.5,
  lower.tail = TRUE
)

dgenlog_sk(x, a = sqrt(2/pi), b = 0.5, p = 2, mu = 0, skew = 0.5)

qgenlog_sk(
  k,
  a = sqrt(2/pi),
  b = 0.5,
  p = 2,
  mu = 0,
  skew = 0.5,
  lower.tail = TRUE
)

rgenlog_sk(n, a = sqrt(2/pi), b = 0.5, p = 2, mu = 0, skew = 0.5)

Arguments

a, b, p

parameters \(\le 0\), with restrictions.*

mu

mu parameter

skew

skewness parameter limited to the interval (-1, 1)

lower.tail

logical; if TRUE (default), probabilities are \(P[X \le x]\) otherwise, \(P[X > x]\).

x, q

vector of quantiles.

k

vector of probabilities.

n

number of observations. If length(n) > 1, the length is taken to be the number required

Value

dgenlog_sk gives the density, pgenlog_sk gives the distribution function, qgenlog_sk gives the quantile function, and rgenlog_sk generates random deviates.

The length of the result is determined by n for rgenlog_sk, and is the maximum of the lengths of the numerical arguments for the other functions.

Details

The used distribution for this package is given by: $$f(x) = 2*((a + b*(1+p)*(abs(x-mu)^p))*exp(-(x-mu)*(a+b*(abs(x-mu)^p))))/ ((exp(-(x-mu)*(a + b* (abs(x-mu)^p)))+1)^2) * ((exp(-(skew*(x-mu))*(a+b*(abs(skew*(x-mu))^p)))+1)^(-1)) $$

The default values for a, b, p and mu produces a function with mean 0 and variance close to 1.

*Restrictions:

If p equals to 0, b or a must be 0 otherwise there is identifiability problem.

The distribution is not defined for a and b equal to 0 simultaneously.

References

Rathie, P. N. and Swamee, P. K (2006) On a new invertible generalized logistic distribution approximation to normal distribution, Technical Research Report in Statistics, 07/2006, Dept. of Statistics, Univ. of Brasilia, Brasilia, Brazil.

Azzalini, A. (1985) A class of distributions which includes the normal ones. Scandinavian Journal of Statistics.

Examples

pgenlog_sk(0.5) 
#> [1] 0.512874
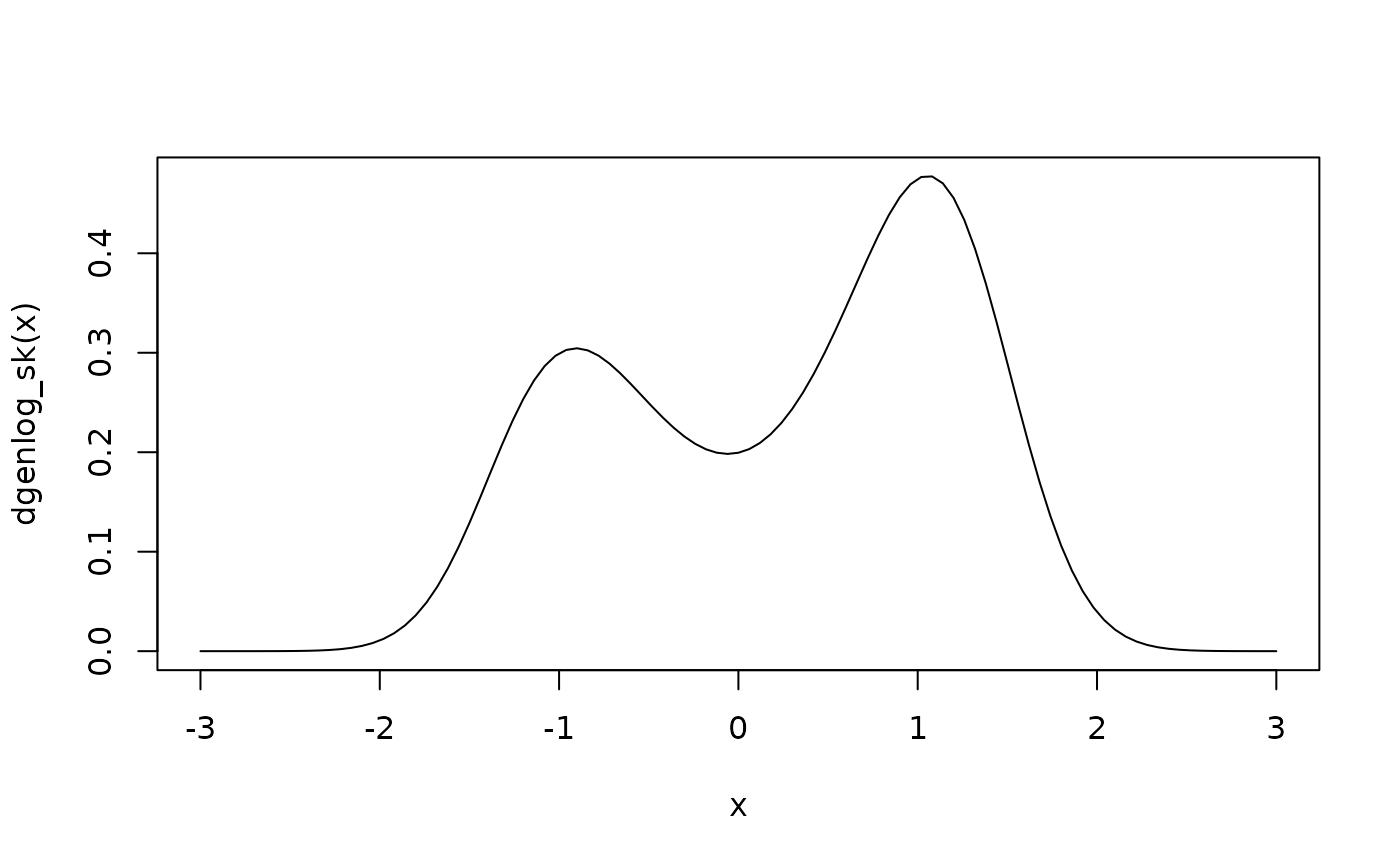
curve(dgenlog_sk(x), xlim = c(-3,3)) 


rgenlog_sk(100) 
#>   [1]  0.12247395  0.90435157  0.48279731  0.88564644  0.49646361  1.26186121
#>   [7]  0.98988890  1.35625905 -1.68172161  1.39396273  2.07306802  0.45760000
#>  [13] -0.17283140  1.12874571  0.70609585  0.82617651  1.31692838  0.65978939
#>  [19] -0.62677627  1.48646541  1.33863630 -0.64298431  0.04715436  1.11757804
#>  [25] -1.07873673 -0.82821709 -0.92740401  0.89192668  1.31179547  1.51320055
#>  [31]  0.61969357  0.68685802  0.94454405 -0.65673995 -1.39457877  1.45749253
#>  [37] -1.26570928  2.09582489  0.77412296 -0.90115981  1.45619929 -1.43804848
#>  [43]  0.72915886 -0.68425487  1.44646644  1.22398682  0.97094585 -0.74315619
#>  [49]  1.03026130 -0.75310120  0.29170717 -0.29849971  0.66371977 -0.62966615
#>  [55]  0.32342272  1.48265911  1.73877848  1.22445496  1.43623703  0.69807017
#>  [61]  1.12471530  2.03111307  0.99450830 -0.76037855 -0.47736701  1.01719609
#>  [67]  1.33677394 -0.67904454 -1.83609908  1.57910371  0.21386110  1.07759612
#>  [73]  0.90204440  0.07222477 -0.21069513  1.05140704  0.89430064 -1.20526787
#>  [79]  1.31071279 -1.23881816  1.30272010 -1.12537337  0.40306750 -0.64774921
#>  [85]  0.94266025 -0.93051396  1.62128484 -0.34848794 -0.16012017  1.39250672
#>  [91]  1.24458420 -1.14620221  1.44571226  1.12412732 -0.05055590  2.36716793
#>  [97] -0.22016494  1.59569070 -0.75644893 -1.47439076

qgenlog_sk(0.95)
#> [1] 1.607905